Page 33 - การสำรวจ

2-16

ี่
10.2.1 ค่าเบี่ยงเบนมาตรฐาน คือ ค่าทเบี่ยงเบนจากค่าเฉลี่ยโดยมีความน่าเป็นของ
การวัดเท่ากับ 0.6827 ค่าเบี่ยงเบนมาตรฐาน หาจากสมการต่อไปนี้

∑(x - x) 2
̅
i
 = ±√
(n - 1)
่
กรณีการวัดมีระดับความน่าเชื่อถือไม่เทากัน จะต้องนําค่าน้ำหนักมาคิดด้วยดังนี้
∑w (x - x) 2
̅
i i
 = ±√
(∑w)(n-1)
i
้
ี่
10.2.2 ค่าคลาดเคลื่อนสุ่มเป็นไปได คือ ค่าทเบี่ยงเบนจากค่าเฉลยโดยมีความน่าเป็น
ี่
ี่
้
ของการวัดเท่ากับ 0.5 ค่าคลาดเคลื่อนสุ่มทเป็นไปไดสามารถหาจากค่าเบี่ยงเบนมาตรฐานดังนี้
E = ±0.6745
p

์
ตัวอย่างที่ 2.3 การวัดระยะทางระหว่างจุด 2 จุดด้วยเครื่องวัดระยะอิเล็กทรอนิกสจำนวน 10 ครั้ง ได ้
ื่
ี
ค่าดัง ตาราง จงหาระยะทางที่ดทสุด ค่าเบี่ยงเบนมาตรฐาน และค่าคลาดเคลอนเป็นไป
ี่
ได
้
ครั้งที่ 1 2 3 4 5
ระยะทาง (ม.) 574.467 574.46 574.469 574.465 574.471
ครั้งที่ 6 7 8 9 10

ระยะทาง (ม.) 574.461 574.463 574.466 574.46 574.468

่
้
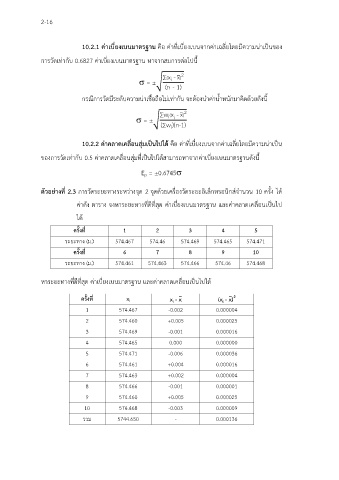
หาระยะทางที่ดีที่สุด ค่าเบี่ยงเบนมาตรฐาน และคาคลาดเคลื่อนเป็นไปได
2
ครั้งที่ x x - x ̅ (x - x)
̅
i
i
i
1 574.467 -0.002 0.000004
2 574.460 +0.005 0.000025
3 574.469 -0.001 0.000016
4 574.465 0.000 0.000000
5 574.471 -0.006 0.000036

6 574.461 +0.004 0.000016
7 574.463 +0.002 0.000004

8 574.466 -0.001 0.000001
9 574.460 +0.005 0.000025
10 574.468 -0.003 0.000009

รวม 5744.650 - 0.000136